11ºC/12ºA Distância entre Planos - conclusão

Ora cá está .... depois de determinado o segmento BI é só determinar a sua v.g. com uma simples mudança de planos

11ºC/12ºA Distância entre Planos

A pedido do André Dias e porque hoje estou bem disposto.

Resolução da aplicação da aula passada.
Pretende-se a determinação da distância entre dois Planos paralelos alfa e beta; alfa está definido por uma sua recta de maior declive; beta é dado por um ponto.
1ª hipótese de resolução - considerando os traços dos Planos (convenhamos que é fraquinha ... os craques vão lá com as rectas de frente e nível até porque os traços dos planos podem não estar nos limites do desenho. O André vai pagar esta postagem com essa aplicação.)

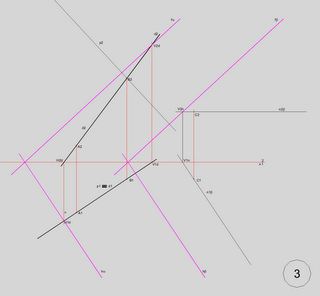
Então, a partir dos dados determinamos os traços de alfa;

Se beta é paralelo a alfa as rectas de nível dos planos também são paralelas; por C passamos uma recta de nível que nos permite determinar os traços de beta;

Para determinarmos a distância entre os planos vamos utilizar uma recta que lhes seja ortogonal, já que a distância entre os planos fica determinada pelo segmento cujos extremos são os pontos de intersecção dessa recta com os planos; como - muito inteligentemente - o Bruno observou na aula, se essa recta passar por um dos pontos de qualquer dos planos, uma das intersecções fica determinada ... é menos trabalho; eu optei por passá-la por B, de alfa;

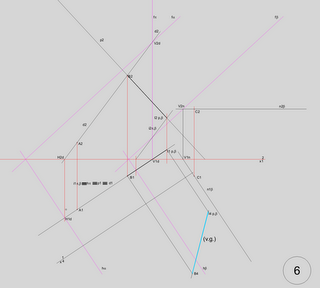
Reparem que como as projecções de p têm que ser ortogonais aos traços dos planos (condição da recta ortogonal a um plano) p1 fica coincidente com d1 ... é só poupar; agora só temos que determinar a intersecção de p com beta; recorrendo ao método (há aí uma postagem sobre isso) utilizei o plano vertical que é projectante de p;

Agora é só determinar a intersecção;

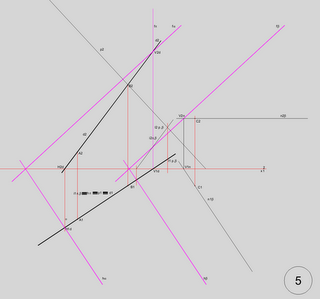
Com esta determinada, temos o segmento BI cuja verdadeira grandeza - com uma simples mudança de planos .... (como veremos noutra postagem que esta já não admite mais imagens ....)

Atenção 11ºC/12ºA

Eu sei que estão todos muito tristes por hoje não ter havido aula. Como é provável que amanhã também não haja, o teste fica adiado para a próxima 3ª feira...

Até lá e porque não quero que vos falte nada ...ou morram de tédio ... vai um novo exercício que é uma variante do anterior (a propósito, alguém já o resolveu?)

Defina beta, passante, que é ortogonal a alfa dado por i, de maior inclinação, a que pertencem A(0; 5; 1) e B(-3; 1; 3).

Nota: como beta é passante fica definido por um ponto ou por uma qualquer recta.

A mesma observação que para o anterior .... se começarem a deitar fumo ....

11ºE Mudança de Planos

Recapitulando a aula de hoje...

Em GD a resolução de determinado tipo de problemas, como a determinação de verdadeiras grandezas, em geral, tem que ser realizada com operações que se designam, habitualmente, por métodos auxiliares.
As Mudanças dos Planos de Projecção, as Rotações e os Rebatimentos (caso particular das Rotações) são as variantes desses métodos.

Na aula de hoje vimos, na generalidade, em que consistem esses métodos e começámos a desenvolver o método da Mudança de Planos.

Na imagem seguinte podemos constatar que a verdadeira grandeza (v.g.) de qualquer segmento que pertencesse a r não seria legível nas suas projecções já que a recta é oblíqua.



Também vimos que a v.g. só é "legível" em projecção num Plano a que a recta seja paralela. Se, por exemplo, a recta estiver de nível ou de frente.
Vamos alterar, então, a posição da recta relativamente aos Planos de Projecção para que fique, por exemplo, de frente - ou seja, paralela ao PVP.
Temos, por isso que mudar o PVP para uma nova posição tal que a recta lhe seja paralela.
Quando suprimimos o PVP- imagem seguinte - repare que mantemos tudo o que relaciona a recta com o PHP - a sua projecção horizontal e a sua cota não se alteram ...


Por uma questão de referência visual mantivemos o eixo x original

A próxima imagem já nos mostra o PVP na posição em que o queremos - paralelo à recta ...


Note-se, agora, que temos "coisas novas":

• um novo eixo dos x - x';
• uma nova projecção vertical (r4);
• o afastamento da recta, que é agora constante.

Com esta operação a projecção vertical de q.q segmento que pertença à recta pode se "lido" em v.g..

Na próxima imagem, o "boneco" do quadro com a mesma operação em DPO



Alguém se lembra porque é que a nova projecção da recta se designa por r4?
Então que responda num comentário (vale pontos)
Bom trabalho

Mais um Prof "bloguista"

Era bom que a moda pegasse ...
Pois é, mais um Prof. da Bordalo com blog de apoio aos alunos.
Mesmo que não tenham a disciplina de Geografia vale a pena visitarem o http://geografianabordalo.blogspot.com do Prof António José Xavier. Está bom e interessante .... e propõe discussão de questões actuais.

Com pequenas coisas se vão construindo futuros sólidos ...

11ºC/12ºA Novo problema

Este também é giro ...... e mais fácil do que o que fizemos em aula.


Represente pelos seus traços um plano oblíquo, gama, perpendicular a alfa, passante, sendo:

• alfa definido por A(0; 4; 2);
• gama a que pertence G(-5; 6;5) e cujo traço horizontal faz com x 45º a.p.d.

Já agora e começando a aquecer os motores para os problemas métricos que são já...já a seguir:

• que ângulo fará gama com o P.H.P? .... eu sei que é chato, mas como vai estar mau tempo .... e com o P.V.P.?

Só para ajudar, a solução é simples .... se começarem a deitar fumo é porque estão longe ...

Bom fim-de-semana!